Lecture 21- Intractability I

Last time, we finished looking at reductions and just began to loop into the complexity class NP. In this lecture, we will cover:

NP problems
- Oracles, certificates, polytime verification algorithms
- 2 problems in NP
  - Subset sum
  - Hamiltonian Cycle
Relationship between P and NP
Polynomial transformations

Complexity Class NP → Non-deterministic Polynomial Time

Recall that last example from last class → subset-sum problem. We wrote a polytime verification algorithm for the Oracle. Recall it is:

# given such an oracle, this algorithm would solve subset-sum
def SubsetSumWithOracle(I): 
	C = Oracle(I)
	return verify(I,C)
 
def verify(I, C):
	if C not subset of I then return false
	return (sum(C) == 0)

→ Dumb Sub-set Sum Algorithm:

Pretend we are the oracle, and make certificates. For this problem, the type of certificate: set of integers.
Say we had the following dumb sub-set sum algorithm:

def SubsetSum(X[1...N]):
	for every possible subset S of X:
		if sumzToZero(S) then return True
	return False

This algorithm generates every possible subset’s certificate
For each one, verify $S$ → sumToZero(S)
If any certificate $S$ sums to 0 → a yes-certificate, and we return True
A certificate that does not sum to 0 doesn’t really prove anything (would need to know all certificates sum to 0)
Generating all certificates is expensive (exponential time) → but verifying one is polytime on input size
If there was such a thing as a no-certificate, what would it look like? How long would it take to verify it?

→ Formal Definition of Certificates

Certificate: Informally, a certificate for a yes-instance $I$ is some “extra information” $C$ which makes it easy to verify that $I$ is a yes-instance
- A “yes-instance” refers to a specific input for a decision problem for which the answer is “yes.”
- For subset sum → you could give a subset that you claim sums to 0
Certificate Verification Algorithm: Suppose that Ver is an algorithm that verifies certificates for yes-instances. Then Ver(I,C) outputs “yes” if $I$ is a yes-instance and $C$ is a valid certificate for $I$ . If Ver(I,C) outputs “no”, then either $I$ is a no-instance, or $I$ is a yes-instance and $C$ is an invalid certificate
In the case of NP problems:
- The verifier algorithm takes both the input and the certificate as its input.
- It checks, in polynomial time, whether the combination of the input and the certificate is valid and satisfies the conditions for a “yes-instance.”
The key characteristic of problems in NP is that, while finding a certificate (solution) might be computationally challenging, verifying a given solution is computationally easy.

→ Generalizing beyond Subset-sum

You can solve any decision problem in non-deterministic poly-time given:
1. A poly-time non-deterministic oracle, and
2. A poly-time **verify** algorithm

Such that
1. If $I$ is yes-instance → oracle returns a yes-certificate $C$
2. If $I$ is a no-instance → verify(I,C) returns False for all $C$

Defining NP

A decision problem $Π$ is solved solved by a poly-time verify algorithm. iff (note, “solved” is being defined here, we’re not trying to say if finds a solution for):

for every yes-instance $I$ , there exists a certificate $C$ such that verify(I,C) returns True (that proves the answer is yes) ,and

for every no-instance $I$ , verify(I,C) returns False for every $C$

When we say an NP problem is “solved,” we mean that there exists a polynomial-time verifier algorithm that can efficiently check the correctness of a solution (certificate) for any given instance of the problem.

The above definition is crucial → when we are asked to show a problem is in NP → this is what we need to show

The complexity class NP denotes the set of all decision problems that could be solved by poly-time verify algorithms

So, in P, the emphasis is on the efficiency of finding a solution, while in NP, the emphasis is on the efficiency of verifying a solution. The distinction is important in understanding the nature of problems and the classes they belong to in complexity theory.

Note: it is not necessary to be able to implement an oracle for a problem to be in NP → we can simply assume an oracle exists, and show a poly-time verify algorithm exists

→ Mechanics of Showing a Problem is in NP

How to show $Π \in NP$
1. Define a type of certificates
2. Design a poly-time verify(I,C) algorithm
3. Correctness proof:
  1. Case 1: Let $I$ be any yes-instance; find $C$ such that verifty(I,C) is True
  2. Case 2: Let $I$ be any no-instance, and $C$ be any certificate → prove verify(I,C) is False

→ We Show this more throughly through another example → showing HC Cycle problem is NP

Another example: Hamiltonian Cycle

Instance: An undirected graph $G = (V, E)$
Question: Does $G$ contain a hamiltonian cycle?

Let’s show this problem is in NP! We are looking to find a poly-time verify algorithm…

Type of certificate? → Array of nodes, which may or may not represent a Hamiltonian Cycle
How to verify that given an array of nodes, they represent a Hamiltonian cycle.

def HamiltonianCycleVerify(G=(V,n,E,m), X):
	if size(X) is not n then return False
	used[1...n] = array containing all False
	
	for i = 1 .. n:
		if used[X[i]] then return False
		used[X[i]] = true
	
	for i = 1 ... (n-1):
		if no edge X[i] to X[i+1] then return False
	if no edge X[n] to X[1] then return false
 
	return True

This is a verify algorithm we imagine being called on the certificate $X$ produced by oracle(G)
Correctness proof:
- Case 1: If $G$ is a yes-instance of the problem → find some certificate $X$ for which this procedure returns true
  - If $G$ is a yes-instance, there is a hamiltonian cycle. Suppose $X$ is a sequence of n consecutive nodes on that cycle → then this returns true
- Case 2: If $G$ is a no-instance of the problem → every certificate should cause verify to return False
  - ==Almost always, we prove the contrapositive==
    - If some certificate verify returns true, then $G$ is a yes-instance
    - If we return true, then the graph contains cycle with n distinct nodes → proves existence of HC in $G$ , which means $G$ is a yes-instance

$P \subseteq NP$
- Consider a problem $Π \in P$
- We show there exists a poly-time verify(I,C) SUCH THAT:
  - For every yes-instance $I$ of $Π$ , verify(I,C) = true for some $C$
  - For every no-instance $I$ or $Π$ , verify(I,C) = false for all $C$
- By definition, there is a poly-time algorithm $A$ to solve $Π$
  - Implement verify(I,C) by simply running $A (I)$ → ignoring $C$
  - We can completely disregard the certificate since we can already solve this problem in poly-time on every input. So we just run the algorithm on the input
  - Regardless of what $C$ is, verify(I,C) satisfies the above
How about $NP \subseteq P$ → Million dollar question. We strongly suspect it is not, we cannot solve it

Polynomial Transformations

→ A subclass of poly-time reduction commonly used for NP-completeness and impossibility results

So whats a polynomial transformation?
Some previous transformations we have seen the are reductions in previous lectures
A polynomial transformation is a like a special case of a poly-time reduction where we transform the input once and we call the oracle once, and we return the value the oracle returned. Single call to oracle is key here.

→ Here is the formal definition

For a decision problem $Π$ , let $I (Π)$ denote the set of all instances of $Π$ . Let $I_{yes} (Π)$ and $I_{n o} (Π)$ denote the set of all yes-instances and no-instances respectively of $Π$ .
Suppose that $Π_{1}$ and $Π_{2}$ are decision problems. We say that there is a polynomial transformation from $Π_{1}$ to $Π_{2}$ (denoted $Π_{1} \leq_{P} Π_{1}$ ) if there exists a function: $f : I (Π_{1}) \to I (Π_{2})$ such that the following properties are satisfied:
- $f (I)$ is computable in poly-time (as a function of $S i ze (I)$ , where $I \in I (Π_{1})$ )
- If $I \in I_{yes} (Π_{1})$ , then $f (I) \in I_{yes} (Π_{2})$
- If $I \in I_{n o} (Π_{1})$ , then $f (I) \in I_{n o} (Π_{2})$
- The above 2 is saying → after transforming $Π_{1}$ ’s input, you can run a solution to $Π_{2}$ and just return the result
Mechanics → to give a polynomial transformation, you must:
1. Specify $f (I)$ (we’ll have to write this function $f$ in code)
2. show it runs in poly-time, and
3. show $I$ is a yes-instance of $Π_{1}$ IFF $f (I)$ is a yes-instance of $Π_{2}$

But, how do we argue the 3rd point in the above?

A polynomial transformation can be thought of as a (simple) special case of a polynomial-time Turing reduction, i.e. if $Π_{1} \leq_{P} Π_{2}$ , then $Π_{1} \leq_{P}^{T} Π_{2}$ . Given a polynomial transformation $f$ from $Π_{1}$ to $Π_{2}$ , the corresponding Turing reduction is as follows:
- Given $I \in I (Π_{1})$ , construct $f (I) \in I (Π_{2})$
- Given an oracle for $Π_{2}$ , say $A$ , run $A (f (I))$ and return whatever the result is
Basically, we transform the instance, and then make a single call to the oracle
Very important point → we do now know whether $I$ is a yes-instance or a no-instance of $Π_{1}$ when we transform it to an instance of $f (I)$ of $Π_{2}$ . So, we can’t use this kind of information in the transformation.

Let’s see an example of this. Consider the following problems:

So, lets do a transformation from the clique problem to the vertex cover problem.

→ Clique $\leq_{P}$ Vertex-Cover

Suppose $I = (G, k)$ is an instance of Clique where $G = (V, E), V = {v_{1}, ..., v_{n}}$ and $1 \leq k \leq n$
Construct instance $f (I) = (H, n - k)$ of Vertex-Cover, where $H = (V, F)$ and $v_{i} v_{j} \in F ⟺ v_{i} v_{j} \in / E$

→ Proving this is a Polynomial Transformation

We denote Clique by $C L$ and Vertex-Cover by $V C$
$C L \leq_{P} V C$ IFF there exists $J (C L) \to J (V C)$ such that:
1. $f (I)$ is computable in poly-time, for all $I \in J (C L)$
2. If $I \in J_{yes} (C L)$ then $f (I) \in J_{yes} (V C)$
3. If $f (I) \in J_{yes} (V C)$ then $I \in J_{yes} (C L)$

(1) Let’s first show that first point → $f (I)$ is computable in poly-time. The following slide shows this.

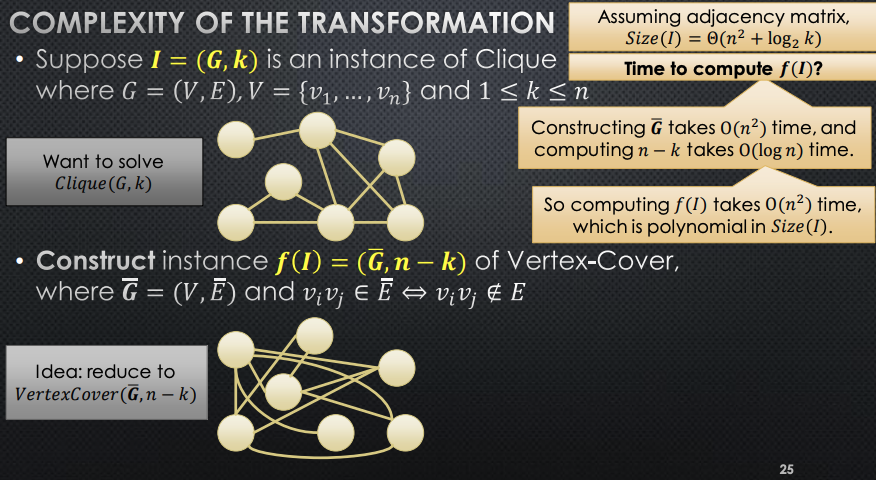
So the mapping is clearly polynomial in the input size.

(2) If $I \in J_{yes} (C L)$ then $f (I) \in J_{yes} (V C)$

(3) If $f (I) \in J_{yes} (V C)$ then $I \in J_{yes} (C L)$

💻 Allan Yin's Blog

Explorer

Lecture 21- Intractability I

Complexity Class NP → Non-deterministic Polynomial Time

Defining NP

Another example: Hamiltonian Cycle

Polynomial Transformations

Graph View

Table of Contents

Backlinks

💻 Allan Yin's Blog

Explorer

Lecture 21- Intractability I

Complexity Class NP → Non-deterministic Polynomial Time

Defining NP

Another example: Hamiltonian Cycle

How are P and NP related

Polynomial Transformations

Graph View

Table of Contents

Backlinks