Lecture 18- Applications of Max Flow

Max Bipartite Matching

We have looked at bipartite graphs before → can be partitioned into 2 sets. We are interested in finding a maximum matching (or a maximum cardinality of the matching).

• Input: a bipartite graph $G=(X,Y,E)$
• Output: a maximum cardinality set of edges that are vertex disjoint

A set $S$ of edges is called a matching if no 2 edges in $S$ share a vertex. A matching is a perfect matching if every vertex is matched

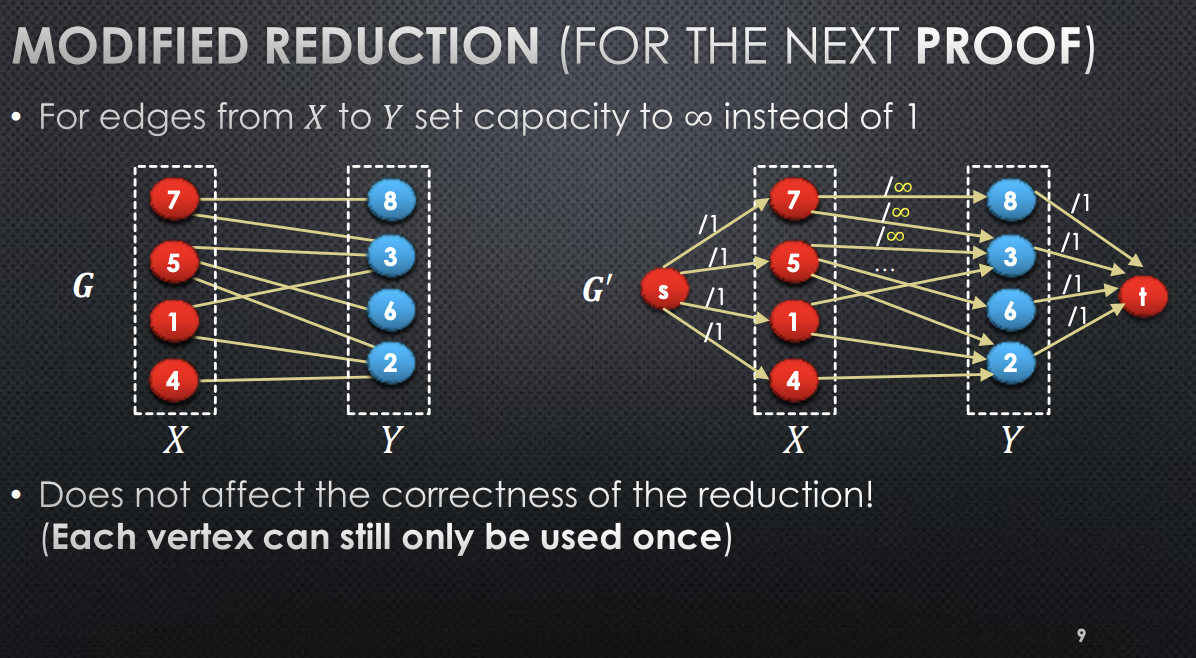
An interesting property is that we can reduce a bipartite graph into a max flow problem. Given a bipartite graph $G=(X,Y,E)$, construct $G^{\prime }=(V^{\prime },E^{\prime })$ as follows:

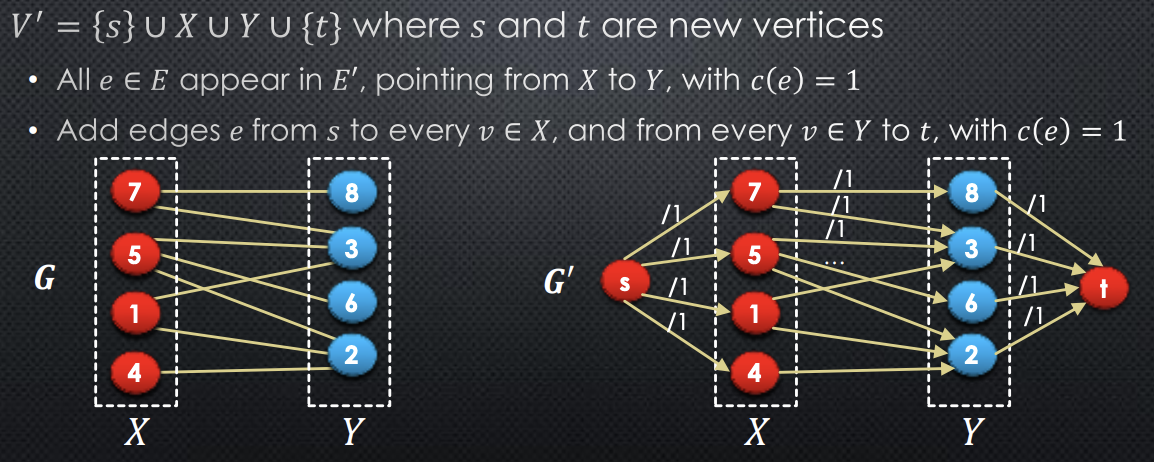
So, lets prove this reduction is correct.

→ Claim: there is a matching of size $k$ IFF there is an s-t flow of value $k$ in $G^{\prime }$

• → clearly, if there is a matching of size $k$, there is a flow of size $k$, and is trivial given the graph

  

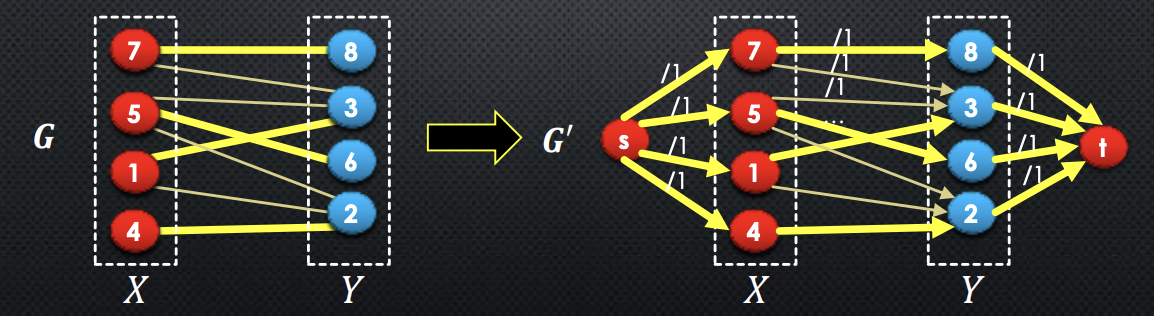
• ← let’s show if there is a flow of size $k$, then there is a matching of size $k$

  • Proof:

  • We decompose the flow into $k$ capacity-disjoint st-paths, each with flow 1

  • Each path is 3 edges: $s\to X,X\to Y,Y\to t$

  • Each edge from $s\to X$ and $Y\to t$ has capacity 1

  • So, each vertex, except for $s,t$ can be used on at most one path

  • Removing edges $s\to X$ and $Y\to t$ gives $k$ vertex-disjoint edges → thus, our original bipartite graph matching

    

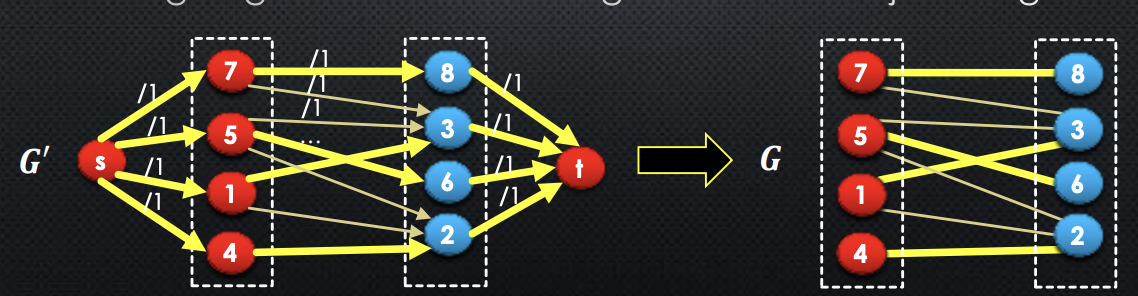
→ Complexity

---

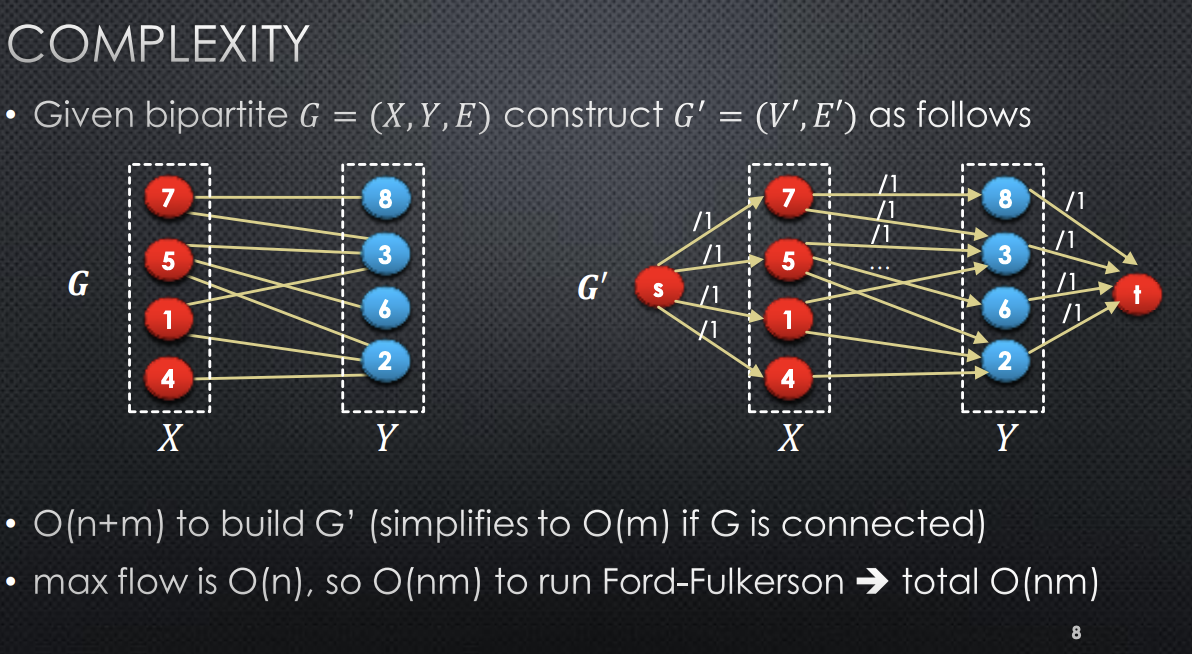
Minimum Vertex Cover

• Vertex Cover: given a graph $G=(V,E)$, a set $S$ of vertices is called a vertex cover IFF for every $(u,v)\in E$, either $u\in S$ or $v\in S$

  • Minimum Vertex Cover: what is the smallest $k$ such that there exists a vertex cover $S$ with $|S|=k$. Minimum $k$ is the minimum vertex cover

→ König’s Theorem

This theorem states that $\text{|Max Matching| = |Min Vertex Cover|}$

• What we want to do is ⇒ Let $k=\text{|Max Matching|}$ in $G$. Show $\exists$ a vertex cover of size $k$
• Recall that we can reduce the problem of maximum matching to a problem of max-flow
• since the max st-flow in $G^{\prime }$ is $k$, by max-flow min-cut, there is an st-cut $S$ in $G^{\prime }$ with capacity $k$
• This flow must cross the cut to reach $t$, and it must consume $k$ units of capacity crossing the cut
• There are 3 cases in which capacity can possibly cross the cut:
  1. It can cross the cut going from $s$ to $X$
  2. It can cross the cut going from $X$ to $Y$
  3. It can cross the cut going from $Y$ to $t$
     1. Case 2 is not possible (recall the above modification, making edges from $X$ to $Y$ equal to $\infty$
• Cases $s$ to $X$:
  • we go via an edge from $s$ to $X-S$ (elements in $X$ but not in $S$) with capacity 1
• Cases $Y$ to $t$:
  • same reasoning as above. We go via en edge from $Y\cap S$ to $t$ with capacity 1
  • So, $k$ = capacity crossing the cut = # of such edges = total # vertices in → $(X-S)\cup (Y\cap S)$